Solving systems of equations by graphing is an essential algebraic method. It offers a visual approach to finding solutions, making it intuitive for learners. Worksheets, such as those from Kuta Software, provide structured practice. Downloadable PDF resources make it convenient for students to master this skill.
1.1 Definition and Importance of Systems of Equations
A system of equations consists of two or more equations with the same variables, aiming to find values that satisfy all equations. It is crucial in modeling real-world problems, such as budgeting, resource allocation, and physics. Solving systems visually through graphing helps identify intersections, which represent solutions. This method enhances problem-solving skills and provides a clear, intuitive approach for understanding complex relationships between variables. Worksheets, like those from Kuta Software, offer structured practice, making it easier to master this fundamental algebraic concept.
1.2 Overview of Graphing as a Method for Solving Systems
Graphing is a visual method to solve systems of equations by plotting each equation on a coordinate plane. This approach involves solving each equation for y, graphing the lines, and identifying their intersection point, which represents the solution. It is particularly effective for linear systems and provides an intuitive way to understand how equations interact. Worksheets, such as those from Kuta Software, often include step-by-step guides and practice problems to help students refine their graphing skills and accurately determine solutions through visualization.
1.3 Benefits of Using Worksheets for Practice
Worksheets are invaluable for mastering systems of equations by graphing. They provide structured practice, helping students refine their graphing skills and understand solution concepts. Printable PDF resources, like those from Kuta Software, offer convenience and accessibility. Worksheets also facilitate study groups and peer tutoring, promoting collaborative learning. Regular practice with these tools builds confidence and accuracy in solving systems visually, ensuring a strong foundation in algebraic methods. They are ideal for both classroom and independent study settings, catering to diverse learning needs and styles.

Understanding the Basics of Graphing Systems of Equations
Graphing systems involves plotting linear equations on a coordinate plane to find their intersection point, which represents the solution. Accurate plotting ensures clear visualization and correct results.
2.1 What are Linear Equations and Their Graphs?
Linear equations are expressions of the form y = mx + b, where m is the slope and b is the y-intercept. Their graphs are straight lines on a coordinate plane. Worksheets often include plotting these equations to identify solutions. For example, y = 2x + 3 creates a line with a slope of 2 and crosses the y-axis at 3. Understanding these graphs is crucial for solving systems visually, as they form the basis for finding intersections.
2.2 Identifying Slope and Y-Intercept in Linear Equations
Linear equations are expressed as y = mx + b, where m represents the slope and b is the y-intercept. The slope indicates the steepness of the line, while the y-intercept is where the line crosses the y-axis. For example, in y = 2x + 3, the slope is 2, and the y-intercept is 3. Accurately identifying these components is essential for graphing and solving systems of equations, as they determine the line’s position and direction on the coordinate plane.
2.3 Plotting Points on a Coordinate Plane
Plotting points on a coordinate plane is a fundamental skill for graphing systems of equations. Each point is represented as (x, y), where x is the horizontal value and y is the vertical value. To plot a point, locate its x-coordinate on the horizontal axis and y-coordinate on the vertical axis, then mark the intersection. For example, plotting (3, 4) involves moving 3 units right and 4 units up. Accurately plotting points ensures the graph is clear and precise, helping to identify the solution to the system visually.

Step-by-Step Guide to Solving Systems by Graphing
Solve each equation for y, plot both on the same coordinate plane, identify their intersection point, and verify the solution by substitution to ensure accuracy.
3.1 Solving Equations for y to Prepare for Graphing
Solving equations for y is a crucial step in graphing systems. Rearrange each equation to isolate y, ensuring consistency and ease of plotting. For example, rewrite equations like ( y = mx + b ) to identify slope and y-intercept. This step simplifies graphing by allowing you to plot lines directly. Use graphing calculators or software to enter equations in y = form, enhancing accuracy. Always verify solutions by substitution to confirm consistency across both equations and ensure the intersection point is correct. This method is foundational for visualizing systems of equations effectively.
3.2 Plotting Both Equations on the Same Coordinate Plane
Plotting both equations on the same coordinate plane is essential for identifying their intersection. Ensure both axes are labeled and scaled consistently. Identify the y-intercept and slope from the rearranged equations (y = mx + b). Plot each equation as a straight line, using distinct colors or symbols for clarity. This step allows visualization of how the lines relate and where they intersect. Use graphing calculators or software for precision, especially for complex equations. Always check the zoom settings to ensure the entire graph is visible, aiding in accurate intersection identification.
3.3 Identifying the Point of Intersection as the Solution
The point where the two lines intersect represents the solution to the system of equations. Carefully locate this point by visually aligning the lines or using graphing tools. Ensure accuracy by double-checking the coordinates. This point satisfies both equations simultaneously, making it the solution. For verification, substitute the coordinates into both original equations to confirm equality. Worksheets often include grids to aid in precise identification. Using calculators or software can enhance accuracy, especially for complex systems. This step is crucial for confirming the correct solution.
3.4 Verifying the Solution by Substitution
After identifying the intersection point, substitute the coordinates into both original equations to confirm they satisfy both equations. This ensures accuracy, especially when dealing with complex systems. Substitution is a reliable method to verify solutions obtained through graphing. Worksheets often include sections for substitution checks, reinforcing understanding. Technology, like graphing calculators, can assist in performing these verifications quickly and precisely, minimizing errors. This step is essential for confirming the validity of the solution.

Benefits and Limitations of the Graphing Method
The graphing method offers a visual, intuitive way to solve systems of equations, making it ideal for understanding relationships between variables. It is particularly effective for linear systems, providing a clear intersection point. However, it becomes less practical for complex or non-linear systems, where accuracy and scalability are challenges. Despite these limitations, graphing remains a valuable tool for initial problem-solving and visualization, especially when supported by worksheets and technology.
4.1 Advantages of Graphing for Visualizing Solutions
Graphing systems of equations provides a clear, visual representation of solutions, making it easier to understand how equations interact. This method is particularly useful for identifying intersection points, which represent solutions. It also helps in distinguishing between types of solutions, such as single points, no solution, or infinitely many solutions. The visual nature of graphing makes it accessible for learners, especially when using worksheets or calculators with zoom features, ensuring accuracy and precision in identifying solutions. This approach is ideal for educational purposes, as it simplifies complex concepts into observable patterns.
4.2 Limitations of Graphing for Complex or Non-Linear Systems
Graphing becomes less effective for complex or non-linear systems due to difficulty in plotting precise curves. Scaling issues can lead to inaccuracies, making it hard to identify exact solutions. Additionally, non-linear systems may have multiple intersections or no clear points of intersection, complicating the visualization process. This method is also time-consuming for intricate equations, often requiring advanced tools for accuracy. Thus, while graphing excels for linear systems, its limitations for non-linear ones make alternative methods more practical in such cases.

Common Challenges and Errors in Graphing Systems
Common challenges include accurately plotting points, identifying the correct intersection, and handling parallel or coinciding lines, which can lead to errors in determining the solution.
5.1 Difficulty in Accurately Plotting Points
Accurately plotting points is a common challenge, especially for novices. Mislabeling axes, miscalculating intercepts, or misreading values can lead to incorrect graphs. Ensuring precise plotting is crucial, as small errors can misrepresent the system’s solution. Using graph paper and breaking equations into manageable steps can help. Additionally, creating a table of values for x and y can improve accuracy, reducing mistakes and fostering a clear visual representation of the system.
5.2 Identifying the Correct Intersection Point
Identifying the correct intersection point can be challenging, especially when lines are close or equations are complex. Ensuring both equations are accurately plotted is crucial. Small errors in graphing can lead to incorrect solutions. To improve accuracy, students can create a table of values for each equation, plot points carefully, and use graph paper. Double-checking calculations and using a ruler to draw straight lines can also help. Additionally, verifying the solution by substitution is a reliable method to confirm the intersection point’s correctness.
5.3 Challenges with Parallel or Coinciding Lines
Parallel or coinciding lines present unique challenges when solving systems by graphing. Parallel lines never intersect, resulting in no solution, while coinciding lines overlap entirely, leading to infinitely many solutions. Identifying these scenarios requires careful analysis of slopes and y-intercepts. If two equations have the same slope but different y-intercepts, the system has no solution. If both the slope and y-intercept are identical, the lines coincide, and all points are solutions. Precise graphing and attention to detail are essential to correctly interpret these cases and determine the appropriate solution set.

Using Graphing Calculators and Technology
Graphing calculators simplify solving systems of equations by allowing users to input equations, zoom in/out, and quickly identify intersection points, ensuring accuracy and efficiency in problem-solving.
6.1 Steps to Graph Equations on a Calculator
To graph equations on a calculator, start by solving both equations for y. Enter each equation into the calculator using the Y= key. Adjust the window settings to ensure the graph is visible. Press zoom to fit the equations on the screen. Use the 2nd key and Calc to find the intersection point. Follow these steps to accurately graph and identify the solution to the system of equations.
6.2 Using Zoom and Calculation Features for Accuracy
Zoom and calculation features on graphing calculators enhance precision. Pressing zoom 6 adjusts the window to display both equations clearly. Using the 2nd key and Calc allows you to find the intersection point directly. These tools help pinpoint the exact solution, ensuring accuracy. They are especially useful for verifying solutions found through graphing, making the process efficient and reliable for students practicing with worksheets.
6.3 Benefits of Technology for Quick and Precise Solutions
Technology, such as graphing calculators and software, streamlines solving systems of equations. It provides quick, precise solutions and enhances visualization. Calculators allow users to zoom in/out for accuracy, while software offers step-by-step guidance. These tools reduce errors and save time, especially for complex systems. Downloadable PDF worksheets complement tech-based learning, ensuring students master graphing skills efficiently. Technology makes solving systems accessible and engaging, fostering deeper understanding and confidence in problem-solving.

Real-World Applications of Solving Systems by Graphing
Solving systems by graphing applies to real-world scenarios, such as business budgeting, physics, and economics. It helps model and solve practical problems, like cost analysis and resource allocation.
7.1 Practical Examples in Business and Economics
In business, systems of equations can model profit and cost functions. For instance, a company’s revenue and expenses can be graphed to find the break-even point. Similarly, in economics, supply and demand curves are solved graphically to determine market equilibrium prices and quantities. These applications highlight how graphing systems provides clear, actionable insights for decision-making in real-world financial and economic contexts.
7.2 Applications in Physics and Engineering
In physics and engineering, systems of equations are essential for modeling real-world phenomena. For example, projectile motion involves solving equations for horizontal and vertical movement to determine trajectories. Electrical circuits use systems to find currents and voltages at different points. Mechanical systems often require solving equations to analyze forces and displacements. Graphing these systems provides a visual understanding of how variables interact, making complex problems more accessible and easier to solve. Worksheets and graphing methods are invaluable tools for developing these problem-solving skills.
7.3 Everyday Problems That Can Be Modeled by Systems
Everyday problems often involve multiple variables that can be modeled using systems of equations. For instance, budgeting expenses, planning events, or managing resources can be simplified by graphing solutions. Worksheets provide practical exercises to apply these concepts. By solving systems, individuals can determine optimal solutions, such as balancing budgets or scheduling tasks efficiently. Real-world applications make learning systems of equations engaging and relevant, preparing individuals for practical problem-solving in daily life.
Practice Exercises and Worksheets
Practice exercises and worksheets, such as those from Kuta Software, offer structured practice for solving systems by graphing. Downloadable PDFs provide convenient access for mastering the method.
8.1 Sample Worksheets for Solving Systems by Graphing
Sample worksheets, such as those from Kuta Software, provide structured exercises for practicing systems of equations by graphing. They include multiple systems, like y = 2x + 1 and y = -3x ─ 2, allowing students to plot and find intersections. These worksheets often feature step-by-step instructions and answer keys for self-review. Many are available as downloadable PDFs, making them easy to access and print. They cater to various skill levels, ensuring comprehensive practice for mastering graphing systems of equations effectively.
8.2 Downloadable PDF Resources for Practice
Downloadable PDF resources, like those from Kuta Software, offer convenient practice materials for solving systems by graphing. These PDFs are easily accessible, printable, and feature clear layouts. They include multiple systems of equations, such as y = 4x ー 2 and y = -2x + 5, along with blank graphs for plotting. Many resources are free, catering to different grade levels and learning needs. PDFs are ideal for self-study, classrooms, or tutoring, providing ample opportunities to refine graphing skills and understand solution intersections visually.
8.3 Answer Keys and Solutions for Review
Answer keys and solutions are essential for reviewing worksheet problems. They provide step-by-step explanations, ensuring understanding. For example, solutions show how to solve equations for y and find intersections. This feedback helps students identify mistakes, improving their graphing accuracy. Many PDF resources include answer sections, allowing learners to verify their work independently. These tools are invaluable for self-assessment and reinforcing concepts, making them a key part of effective practice routines.
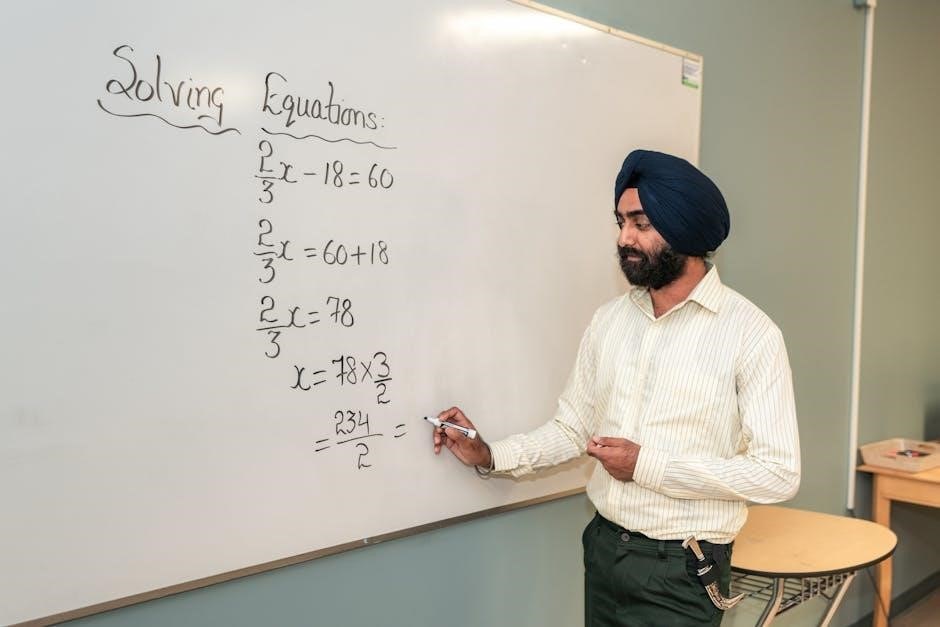
How to Create a Solving Systems of Equations by Graphing Worksheet
Creating a worksheet involves designing problems with clear instructions. Use software like Kuta Software to generate equations. Format for readability and include answer keys for review. Ensure variety in problems to cover different scenarios, aiding comprehensive understanding. This approach helps in effective practice and mastery of graphing systems skills.
9.1 Designing Effective Problems for Practice
Designing effective problems involves creating clear, varied equations. Start with simple systems and progress to complex ones. Include real-world scenarios to enhance relevance. Use Kuta Software to generate equations, ensuring they align with skill levels. Provide step-by-step solutions for review. Incorporate visual aids like graphs to aid understanding. Offer answer keys in PDF format for easy access. Ensure problems cover different slopes and intercepts to build mastery. This structured approach helps students grasp graphing systems efficiently and confidently.
9.2 Formatting for Clarity and Ease of Use
Clear formatting is crucial for effective practice worksheets. Use bold headers to label sections and equations. Organize problems in a grid or table for easy navigation. Provide ample space for graphing, with clear axes and grid lines. Include answer keys in a separate section for quick reference. Ensure equations are large and legible, with sufficient spacing between problems. Use PDF formats to maintain high resolution and clarity when printed. Consistent fonts and spacing enhance readability, making worksheets user-friendly for both students and educators.
9.3 Converting Worksheets to PDF Format
Converting worksheets to PDF ensures universal accessibility and preserves formatting. Use tools like Adobe Acrobat or online converters to maintain layout and clarity. Ensure the PDF file size is optimized, like the 85118-byte example, for easy sharing. Include download buttons for convenience, allowing users to access worksheets quickly. PDFs are ideal for printing and sharing, making them perfect for practice and study groups. This format guarantees that the content remains consistent across all devices, ensuring a seamless learning experience for students.

Tips for Effective Learning and Teaching
Encourage regular practice with worksheets, use graphing calculators for visualization, and promote collaborative study groups. Provide clear examples and feedback to enhance understanding and retention of concepts.
10.1 Strategies for Mastering Graphing Skills
Mastering graphing skills requires consistent practice and a systematic approach. Begin by solving equations for y to easily plot lines. Use Kuta Software worksheets for structured exercises. Incorporate graphing calculators to visualize solutions and verify accuracy. Break complex systems into smaller steps, ensuring accurate plotting of points. Regularly review and correct common errors, such as misidentifying intercepts or slopes. Utilize zoom features for precision and create flashcards to memorize key concepts. Encourage peer tutoring to reinforce understanding and problem-solving techniques.
10.2 Classroom Activities to Reinforce Concepts
Engage students with interactive activities like group graphing sessions, where pairs plot equations on shared charts. Incorporate technology by using calculators for real-time visualization. Assign collaborative problem-solving tasks, such as identifying intersections or distinguishing line types. Create competitions to solve systems quickly and accurately; Use exit tickets to assess understanding and provide immediate feedback. Encourage peer teaching and discussion to clarify doubts. These activities foster collaboration, critical thinking, and practical application of graphing skills.
10.3 Using Worksheets for Peer Tutoring and Study Groups
Worksheets are invaluable for peer tutoring and study groups, fostering collaborative learning. Students can work in pairs to solve systems by graphing, checking each other’s work for accuracy. This encourages discussion and mutual understanding. Study groups can use worksheets to practice collectively, reinforcing concepts like plotting equations and identifying intersections; Peer tutoring enhances problem-solving skills and builds confidence. Worksheets also serve as a shared resource, ensuring everyone practices the same exercises. This collaborative approach strengthens teamwork and prepares students for independent learning.
Solving systems by graphing is a valuable skill, offering visual insights into solutions. Consistent practice with worksheets enhances understanding. Encourage exploration and mastery of this method for long-term success.
11.1 Recap of Key Concepts and Methods
Solving systems of equations by graphing involves plotting lines to find their intersection, which represents the solution. Key steps include solving equations for y, graphing both on the same plane, and identifying the intersection point. Verification by substitution ensures accuracy. Worksheets, like those from Kuta Software, provide practice, while technology tools enhance precision. This method offers a visual understanding, making it ideal for beginners, though it may be less effective for complex systems. Regular practice with PDF resources helps solidify mastery of this fundamental algebraic technique.
11.2 Encouragement for Continued Practice and Exploration
Continued practice is crucial for mastering systems of equations by graphing. Regular use of worksheets and PDF resources builds confidence and understanding. Exploring real-world applications highlights the practical value of this skill. Encourage learners to use technology tools for precision and engage in peer tutoring for collaborative learning. Embrace challenges and view them as opportunities to grow. With persistence, students will become proficient in solving systems of equations by graphing and unlock deeper mathematical insights.